LWDW!

编译原理好鸡儿难，课设真尼玛烦，俺现在只想摸鱼 _(┐「ε:)_

---

前言

对于两个物体之间的碰撞检测，依据两个物体本身属性的不同，所采取的策略也不尽相同。简单的来说可以分为3大类：

1. 依据每一帧中，几何图形的重合来检测
2. 基于像素、地图格子来检测
3. 基于速度矢量与相应判别条件来检测

在弹一弹的例子中，第一种应该是首要的检测方式，后面两种如果俺开心再写吧【滑稽】

而在第一种中，又有几种不同的情形需要采取不同策略对待：

1. 圆-圆
2. 无旋转矩形-无旋转矩形
3. 圆-矩形（可有旋转）
4. 任意多边形

其中1和2都太过耿直，在此不做说明。本水文着重讨论第3种情形，第4种会更的嗯，俺有骗过你么 （’へ’）

圆 & 无旋转方块儿

我们要解决的问题，本质上就是要知道圆与矩形有无“接触”——而有了圆-圆检测的经验后，不难想到，我们要做的就是找到矩形上离圆最近的点，通过这一点到圆心的距离与圆的半径之间的比较，就能确定圆与矩形是否接触：

图片来源：凹凸实验室

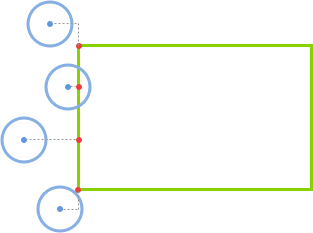
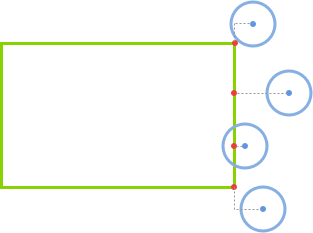
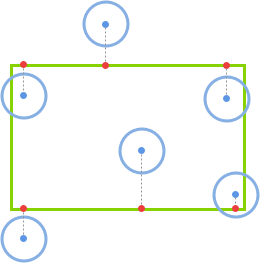
不难看出这个最近点在x轴、y轴与圆心之间的关系，可以参考下面这个demo：

See the Pen rect&ball by Zhouyi (@padfoot_07) on CodePen.

圆 & 旋转方块儿

如果矩形旋转了a度，只需要以矩形中心为旋转中心，旋转画布-a度，我们就又回到了上面一种无旋转情形！

换而言之，我们需要额外做的，就是计算旋转后的圆心。那么首先推导一下某个点绕原点旋转一定角度后的坐标：

证明来源：凹凸实验室

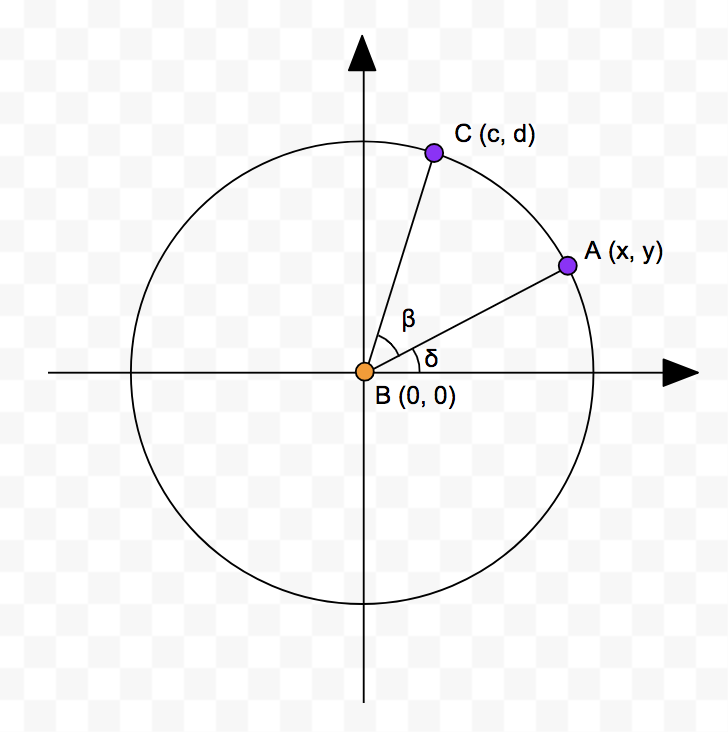
A为旋转前，B为原点，C为旋转后，r为半径，则

1. 设 A 点旋转前的角度为 δ，则旋转（逆时针）到 C 点后的角度为(δ+β)
2. 由于 |AB| 与 |CB| 相等（即长度），且
   • |AB| = y/sin(δ) = x / cos(δ)
   • |CB| = d/sin(δ + β) = c / cos(δ + β)
3. 半径 r = x / cos(δ) = y / sin(δ) = d / sin(δ + β) = c / cos(δ + β)
4. 三角函数两角和差公式：
   • sin(δ + β) = sin(δ)cos(β) + cos(δ)sin(β)
   • cos(δ + β) = cos(δ)cos(β) - sin(δ)sin(β)
5. 得出旋转后的坐标
   • c = r * cos(δ + β) = r * cos(δ)cos(β) - r * sin(δ)sin(β) = x * cos(β) - y * sin(β)
   • d = r * sin(δ + β) = r * sin(δ)cos(β) + r * cos(δ)sin(β) = y * cos(β) + x * sin(β)

那么对于旋转中心 (centerX, centerY) ，其实只要做一个坐标轴平移的工作：

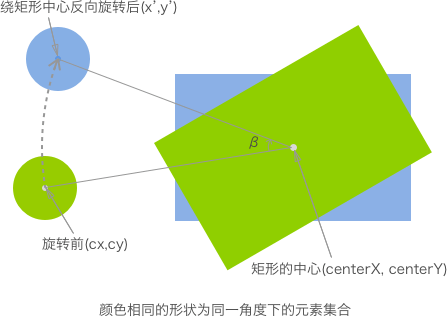
x’ = cos(β) * (cx – centerX) – sin(β) * (cy – centerY) + centerX
y’ = sin(β) * (cx – centerX) + cos(β) * (cy – centerY) + centerY

以上就是我们需要的旋转公式。

下面这个demo中应用了上述理论，透明度较低的是旋转后的图形：

See the Pen rotatedRect&ball by Zhouyi (@padfoot_07) on CodePen.

---

好了不多说了，我只想看下一集小英雄，再见了您！