前言
最近微信弹一弹游戏突然火了,俺又正好在学习相关知识,就来蹭波热点开个系列,拆分一下弹一弹游戏可能涉及到的各种算法或数据结构的实现。当然,估计这个系列更完的时候弹一弹也该凉了嗯。
在弹之前
弹一弹,是一个典型的以碰撞、反弹为核心玩法的游戏。在每一帧计算时,首先要考虑的问题就是涉及的元素是否发生了碰撞,因此也就产生了碰撞检测以及其检测效率的问题,咱先用最耿直的方法来解决这个问题。
两个物体的检测
这还不简单,判断两个物体的碰撞无非是通过各自的x, y位置和宽高等属性计算出两者有无交集。在游戏进行的每一帧中,我们只要计算第一个物体是否碰到了第二个物体。
n个物体的检测
emmmm,由于需要确认他们是否互相碰撞,因此需要一个双重for循环嘛,外层代表这是检测的第n个物体,内层表示他是否与其他的n-1个物体发生碰撞。显然,对于每一帧的检测,时间复杂度是 O(n^2) ;如果我们做一个2d的海洋球池,里面有2000个球,则每帧约需要做4000000次碰撞计算——对于理想的60帧应用,一帧的时间大约是16.6ms,李猜一猜来不来得及算呢?
下面是一个仅涉及碰撞检测的demo,无反弹计算,里面有2000个小球,发生碰撞的球会高亮显示,为了照顾您的cpu,只有点了“开始”按钮后才会开始运算。结论是俺个人的小mac pro跑这个demo约为13帧,对于2帧流畅5帧丝滑的玩家可以说是很厉害了嗯!
See the Pen Silly-ImpactChecking by Zhouyi (@padfoot_07) on CodePen.
引入四叉树
气不气?明眼人都明白,你说左下角和右上角的物体离那么远,有必要去进行检查么?是否有办法,让每个点只需要去检查他附近的一片区域,而不是盲目的去对整片地图内的物体进行检查。换句话说,我们需要一个方法,能高效的获得一片区域内所有的物体。

所以上面是一个看上去很浮夸的图像,可以看到绿框内的点全部都被选中并加亮了,线上demo见codepen。
观察上面的图像,大家可以看出似乎点越密集的地方会分裂出越多的小方块,想必其中是有种奇妙的数据结构在做支撑,那就是俺们的主角——四叉树
WTF is Quadtree
想要实现的策略
在实现四分树前,我们先讲一下往这个平面添加一个个物体的策略,假设容量为4
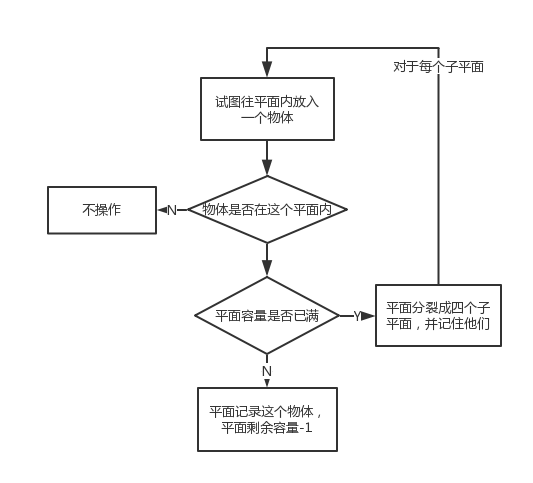
视觉上的表现大概是这样:
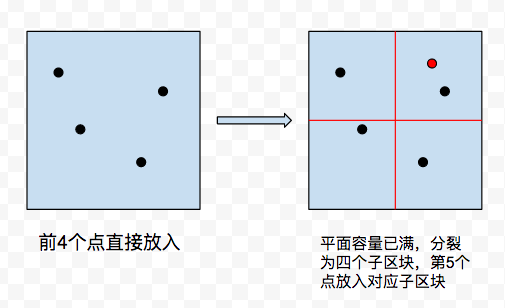
数据结构的实现
为了实现上面的策略,我们引入了四分树这样的数据结构:
class QuadTree {
constructor(boundary, capacity) {
this.boundary = boundary; // 该节点的边界,也就是上文的平面
this.capacity = capacity; // 该节点的容量
this.points = []; // 放入该节点的物体
this.divided = false; // 该节点是否发生了分裂
}
...
}
当我们试图往其中放入一个物体时:
insert(point) {
// 如果物体不在该节点的边界内,直接返回false
if (!this.boundary.contain(point)) return false;
// 如果节点容量有剩余,记录该物体
if (this.points.length < this.capacity) {
this.points.push(point);
}
// 容量已满
else {
// 该节点还未分裂,则进行分裂
if (!this.divided) {
this.subdivide();
}
// 试图将物体放入分裂出的子节点
this.NW.insert(point);
this.NE.insert(point);
this.SW.insert(point);
this.SE.insert(point);
}
return true;
}
上面涉及到了一个重要的操作,节点的分裂:
subdivide() {
// 边界的相关信息
let x = this.boundary.x;
let y = this.boundary.y;
let w = this.boundary.w;
let h = this.boundary.h;
// 获得子节点的边界对象,就是被田字分割的四个子区块
let nw = new Rectangle(x - w / 2, y - h / 2, w / 2, h / 2);
let ne = new Rectangle(x + w / 2, y - h / 2, w / 2, h / 2);
let sw = new Rectangle(x - w / 2, y + h / 2, w / 2, h / 2);
let se = new Rectangle(x + w / 2, y + h / 2, w / 2, h / 2);
// 获得了四个子节点,并记录了他们的引用
this.NW = new QuadTree(nw, this.capacity);
this.NE = new QuadTree(ne, this.capacity);
this.SW = new QuadTree(sw, this.capacity);
this.SE = new QuadTree(se, this.capacity);
// 设置分裂tag
this.divided = true;
}
到此为止,将一个物体放入平面的操作就抽象完毕了,现在回到我们一开始的问题:如何获得一片区域的所有物体?代码已经很直观的说明了:
// 传入一个区域(边界对象)和结果数组(默认为空)
query(range, found = []) {
// 如果节点的边界和区域边界无交集,不处理
if (!range.intersect(this.boundary)) return;
else {
// 对于该子节点记录的所有物体,如果该物体在区域边界内,结果数组记录该物体
for (let p of this.points) {
if (range.contain(p)) found.push(p);
}
// 如果这个节点发生了分裂,对其所有子区块递归查询
if (this.divided) {
this.NW.query(range, found);
this.NE.query(range, found);
this.SW.query(range, found);
this.SE.query(range, found);
}
// 返回结果数组
return found;
}
}
至此,放入&获取的操作便都可以实现了。
那么,想要检查一个物体附近的区域,无非就是以这个物体的坐标、大小为基准创造一个合适的边界作为查询条件,获得他旁边的物体,再进行碰撞的判断。
时间复杂度的考察
啊——所以你构建了一个看起来很酷的数据结构,但是它就比双重循环更好嘛?
我们先考虑对1个物体的检测:大家都知道二分查找,由于每一次查找的区域减半,二分查找的时间复杂度为O(log n);同理,对于四分树的查找,查找的区域会不断的缩小为上一次的1/4,时间复杂度也是O(log n);我们最初的问题是对n个物体之间的碰撞检测,所以这个过程要进行n次,所以借助四分树,查询的时间复杂度降低到了O(n * log n)!爽到!
下面就是应用了四分树的碰撞查询demo,除了在查询时引入了四分树外,其他的操作和上文那卡爆的demo是完全一样的,在俺的小mac上帧数保持在45-55帧:
See the Pen QuadTree-ImpactChecking by Zhouyi (@padfoot_07) on CodePen.
结论
四分树在这个应用中所做的工作是将每个物体需要去检测的邻居物体的范围从整个平面缩小到了我们自己指定的一小片范围,虽然构建四分树也需要时间和空间成本,但收益显然是巨大的 d(`・∀・)b
下一篇讲什么呢——这一篇讲多个物体碰撞检测的效率,下一篇预定为两个物体间碰撞检测的具体实现吧,感觉好难( º﹃º )